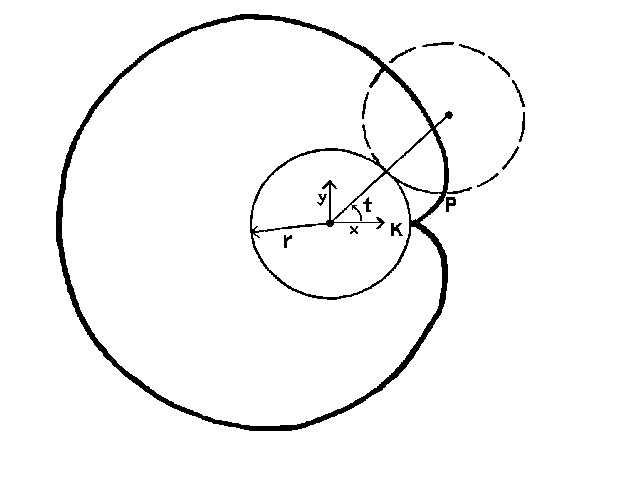Mehr zur Mandelbrot-Menge und ein paar Bilder
Die Grafiken werden durch folgende Parameter bestimmt :
Die Koordinaten des Bildes in der komplexen Zahlenebene :
- Xmin : minimaler Wert der X-Koordinate (der reellen Achse), der linke Rand des Bildes
- Xmax : maximaler Wert der X-Koordinate (der reellen Achse), der rechte Rand des Bildes
- Ymin : minimaler Wert der Y-Koordinate (der imaginären Achse), der untere Rand des Bildes
- Ymax : maximaler Wert der Y-Koordinate (der imaginären Achse), der obere Rand des Bildes
Parameter, die die Rechengenauigkeit regeln bzw. die Einfärbung des Bildes bestimmen :
- Nmax : Zahl der maximal durchzuführenden Iterationen, falls nicht vorher schon durch
den Parameter G (siehe weiter unten) die Rückkopplung abgebrochen wurde. Das heißt
ein Punkt wird nach Nmax Iterationen als zugehörig zur Menge erklärt. Je stärker
die Vergrößerung ist, desto höher sollte Nmax gewählt werden. Sonst
werden die Bilder "unscharf", die Auflösung reicht in diesem Fall nicht aus.
- M : gibt die Farbtiefe an. Das Bild wird mit maximal M verschiedenen Farben
eingefärbt. Ist M größer als 256, so werden die Farbtöne
gegebenenfalls wiederholt, da nur 256 verschiedene Farben zur Verfügung stehen. M muß
immer kleiner als Nmax gewählt werden.
- G : dieser Parameter hat für das Newton-Verfahren eine andere Bedeutung als für
die restlichen Mengentypen :
Mandelbrot-, Julia-Mengen, Biomorphe : Die Rückkopplung wird in der Regel abgebrochen,
wenn sich ein Punkt während der Iterationen mehr als G weit von einem Attraktor
entfernt hat. Je kleiner also G gewählt wird, desto eher wird ein Punkt als nicht zur Menge
gehörig erklärt. Falls das Bild "verschwommen" wirkt (die Ränder werden
immer konturloser, weil auch Punkte als zur Menge gehörig erklärt werden, die nicht dazu
gehören), muß G erhöht werden. Andererseits ist ein größerer Wert
für G nur sinnvoll in Verbindung mit einem größeren Wert für Nmax.
Newton-Verfahren : Auch hier dient G dazu, die Entfernung von einem Attraktor zu
bestimmen, um den Punkt als zugehörig zur Menge oder nicht zugehörig zu erklären. Im
Unterschied zu oben wird die Rechnung aber genauer, wenn G kleiner wird. Für ein
Übersichtsbild reicht ein Wert für G von 0.1 aus. Bei
Ausschnittvergrößerungen sollte G dann entsprechend kleiner gewählt werden
(in Verbindung mit größeren Werten für Nmax!).
Alle Grafiken auf dieser Seite wurden mit einer Auflösung von 640x480 Pixeln
und einer Farbtiefe von 256 Farben mit dem Programm I_M gerechnet.
Übersichtsbild Mandelbrot-Menge (das "Apfelmännchen")
(Geschwindigkeitsdiagramm)
| Xmin | Xmax |
Ymin | Ymax |
Nmax | M | G |
|---|
| -2.4 | 0.8 |
-1.2 | 1.2 |
100 | 80 | 20.0 |

Die Äquipotentiallinien kommen allerdings bei anderer Einfärbung besser zur Geltung:

Der Hauptkörper der Mandelbrot-Menge besteht aus einer sogenannten Kardioide:
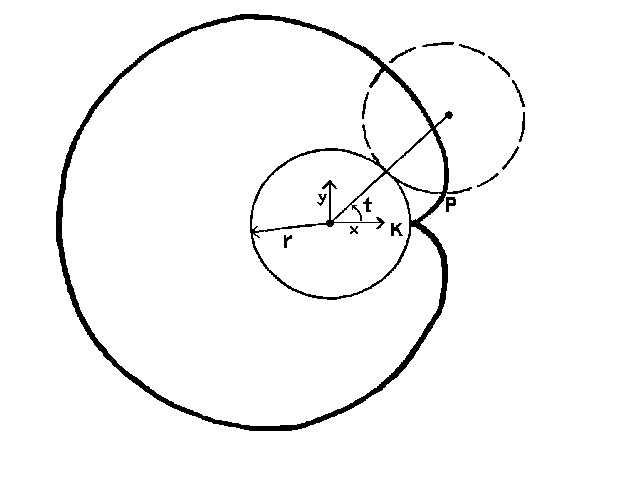
Die Gleichung dieser Kurve lautet (r = 0.25 im Falle der Mandelbrot-Menge):
(x2 + y2) (x2 + y2 - 4rx) - 4r2y2 = 0
oder in Parameterdarstellung:
x = 2r ·cos t(1 + cos t), y = 2r ·sin t(1 + cos t), 0 £ t £ 2p
Die Konstruktion der Kardioide kann man sich so verdeutlichen: ein Kreis liegt mit seinem Mittelpunkt im Ursprung
des Koordinatensystems. Auf diesem Kreis wird nun ein weiterer Kreis mit gleichem Radius abgerollt. An diesem
zweiten Kreis ist im Punkt P ein "Stift befestigt", der während des Abrollvorgangs eine
Spur hinterläßt. Zu Beginn liegt der Stift am Punkt K mit den Koordinaten x = 0, y = 0.25
des ersten Kreises an. Nach einer halben Umdrehung hat P bei x = -0.75, y = 0 seine größte
Entfernung vom Ursprung des Koordinatensystems erreicht. Nach einer vollen Umdrehung ist P wieder bei K
angelangt und die Kurve ist geschlossen.
Weiter ist der "Kopf" der Mandelbrot-Menge ein Kreis mit Radius 0.25 und dem Mittelpunkt bei x = -1, y = 0.
Mit Kenntnis der Gleichung der Kardioide und des Radius ist es nun möglich, die Rechnungen immens zu beschleunigen.
Alle innerhalb der Kardioide und des "Kopfes" liegenden Punkte gehören auf jeden Fall zur Menge.
Für diese Punkte braucht die Rückkopplungsgleichung nun nicht extra durchgerechnet zu werden, sondern sie
können sofort als zur Menge gehörig eingefärbt werden.
Ausschnittvergrößerung der Mandelbrot-Menge
| Xmin | Xmax |
Ymin | Ymax |
Nmax | M | G |
|---|
| -0.7496875 | -0.7296875 |
0.1439375 | 0.1589375 |
1000 | 700 | 20.0 |

Ausschnittvergrößerung der Mandelbrot-Menge
| Xmin | Xmax |
Ymin | Ymax |
Nmax | M | G |
|---|
| -1.98545273549310 | -1.98545273549302 |
0.000609032943788793 | 0.000609032943842352 |
5000 | 4000 | 20.0 |
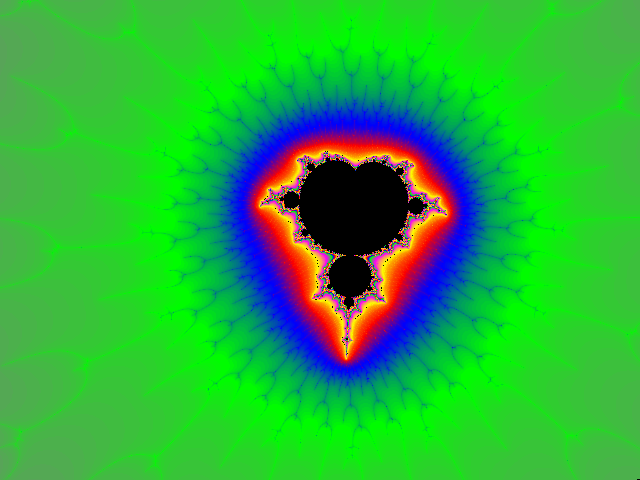
Nachfolgend zwei Grafiken zur Rückkopplungsgleichung zn + 1 = zn6 + c :
Übersichtsbild Mandelbrot-Menge z6
| Xmin | Xmax |
Ymin | Ymax |
Nmax | M | G |
|---|
| -1.53 | 1.53 |
-1.1475 | 1.1475 |
100 | 80 | 20.0 |

Ausschnittvergrößerung aus obigem Bild
| Xmin | Xmax |
Ymin | Ymax |
Nmax | M | G |
|---|
| -0.7496875 | -0.7296875 |
0.1439375 | 0.1589375 |
1000 | 700 | 20.0 |

Zurück zu Fraktale und Chemie
Zurück zur Startseite
Kai Schröder, 29.11.2000