Verhulst-Dynamik
1845 betrachtete P.F. Verhulst als einer der ersten Wissenschaftler die
Entwicklung von Populationen auf mathematischer Basis. Dazu untersuchte er eine
Population, die in der n-ten Generation die Größe xn und in der n + 1
-ten Generation die Größe xn + 1 aufweist. Das relative Wachstum W ist
dann gegeben durch
und wenn W eine Konstante ist, folgt die Rückkopplungsgleichung
Verhulst nahm nun an, daß W selbst wiederum eine Funktion der
Generationenzahl ist, also von xn abhängt und setzte
|
W = w (1 - xn) mit w > 0 (Wachstumsparameter) |
|
Das relative Wachstum der Population wird also immer kleiner, je größer die
Population bereits angewachsen ist. Bei ihrer Maximalgröße (xn = 1) ist das
relative Wachstum gleich Null. Wird das relative Wachstum nun als
definiert, erhält man die Grundform der Verhulst-Dynamik zu
Diese Rückkopplungsgleichung sieht ebenfalls - wie die Gleichung der
Mandelbrot-Rückkopplung - sehr einfach aus und auf den ersten Blick würde man nichts
besonderes erwarten. In Abhängigkeit vom Wachstumsparameter w zeigt sich aber
ein überraschendes Verhalten der Rückkopplung bei Durchführung der Iterationen
(ein Startwert x0 der Population im Bereich größer als 0 und kleiner als 1
sei im folgenden vorausgesetzt; betrachte hierzu auch das Übersichtsbild weiter unten):
- w £ 1 :
-
Die Population wird immer kleiner, bis sie schließlich
ausstirbt, und zwar umso schneller, je kleiner w gewählt wird
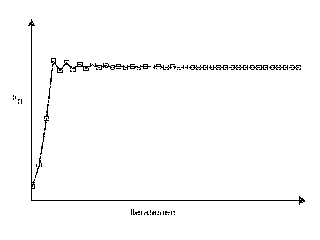
- 1 < w < 3 :
-
Die Population pendelt sich nach mehr oder weniger
Iterationen (Generationen) auf einer konstanten Größe ein. Je größer w,
desto größer auch die Stärke der Population.
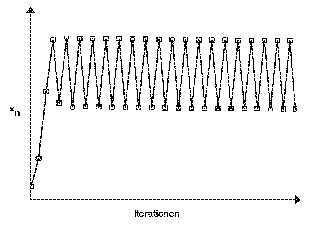
- 3 £ w £ 3,45 :
-
Nach einigen Iterationen bilden sich zwei
verschiedene stabile Populationsniveaus heraus. Die Population schwankt von
einer Generation zur nächsten immer zwischen diesen beiden Werten hin und her.
Man spricht in diesem Zusammenhang von einer sogenannten 'Bifurkation'.
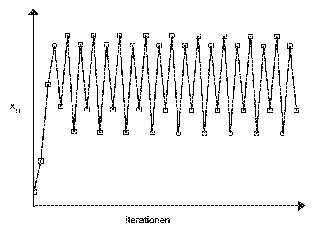
- 3,45 < w £ 3,54 :
-
Jetzt pendelt die Population nach einigen
Generationen immer zwischen vier verschiedenen Werten.
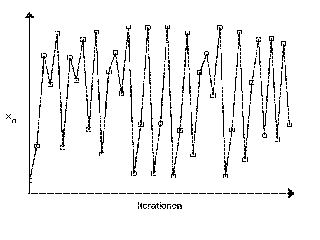
Bei weiterer Vergrößerung von w treten immer mehr stabile Populationsniveaus
auf (es tritt jeweils eine Verdoppelung der Niveaus auf), bis im äußersten
Fall w = 4 die Populationsgröße alle Werte xn zwischen 0 und 1 annehmen
kann und sich ohne erkennbaren Grund überhaupt keine stabilen Niveaus mehr
einstellen. In diesem Zusammenhang spricht man dann von
deterministischem Chaos.
Trägt man in Abhängigkeit vom Wachstumsparameter w die Größe der
Population nach einer größeren Zahl von Generationen auf, erhält man das
sogenannte Feigenbaum-Szenario.
Die Parameter zur Darstellung sind die folgenden:
- Pmin, Pmax : minimaler (in den Bildern unten)
und maximaler (in den Bildern oben) Wert der Größe der
Population, die in der Grafik dargestellt werden sollen.
0 £ Pmin, wenn Pmin = 0 ist die
Population ausgestorben. Und Pmax £ 1 (ein Wert von 1
für Pmax entspricht der maximalen Lebensraum-Kapazität). Es gilt immer :
0 £ Pmin <
Pmax £ 1.
- wmin, wmax : minimaler (in den Bildern links)
und maximaler (in den Bildern rechts) Wert des Bereichs des
Wachstums-Parameter, der dargestellt werden soll. Es gilt immer :
0 £ wmin <
wmax £ 4.
- IE : Zahl der Einschwing-Iterationen. IE-mal wird die
Rückkopplungsgleichung durchlaufen, ohne daß Pixel gezeichnet werden. Erst ab
IE + 1 Iterationen werden die Pixel gesetzt. IE darf nicht zu
klein gewählt werden, weil die Grafik an Bifurkationspunkten sonst "unscharf" wird.
Gerade im Bereich des deterministischen Chaos muß IE recht groß
vorgegeben werden (teilweise größer als 1000, je nach Größe des Ausschnitts).
- NGen : Anzahl der nach IE Einschwing-Iterationen zu berechnenden
Generationen. Gezeichnet werden aber nur die Werte für Generationen (Pixel), die im Fenster
wmin £ wmax liegen. Das bedeutet,
daß NGen umso größer gewählt werden muß, je kleiner
der gewünschte Ausschnitt für P gesetzt ist, damit die Grafik auch aussagekräftig
wird.
Übersichtsbild Verhulst-Dynamik
| Pmin | Pmax |
wmin | wmax
| IE | NGen |
|---|
| 0.0 | 1.0 |
0.0 | 4.0 |
500 | 200 |
 (Anmerkung: für 0 < w < 1
stirbt die Population aus, der weiße Strich links unten im Bild ist aber nicht oder
nur sehr schlecht zu erkennen.)
(Anmerkung: für 0 < w < 1
stirbt die Population aus, der weiße Strich links unten im Bild ist aber nicht oder
nur sehr schlecht zu erkennen.)
Das "meiste Geschehen" spielt sich im rechten Viertel des obigen Bildes ab. Dieser
Bereich ist im folgenden Bild vergrößert dargestellt :
Ausschnittsvergrößerung Verhulst-Dynamik
| Pmin | Pmax |
wmin | wmax
| IE | NGen |
|---|
| 0.0 | 1.0 |
2.99 | 4.0 |
500 | 300 |

Die nachfolgende Grafik zeigt eine Vergrößerung des im oberen Bild rot
begrenzten Bereichs. Die w-Achse (Abszisse) wurde zur
besseren Übersichtlichkeit gegenüber der Vertikalen gestreckt. Wie zu sehen
ist, tritt auch hier wieder das Phänomen der Selbstähnlichkeit auf.

Und noch eine weitere Ausschnittsvergrößerung aus dem Feigenbaum:

Je stärkere Vergrößerungen angefertigt werden sollen, desto mehr Einschwing-Iterationen
und desto mehr Generationen müssen durchgeführt werden, damit die Grafik "sauber"
aussieht. Im letzten Bild wurde IE = 2000 und NGen = 1000
gewählt.
(Die Grafiken auf dieser Seite wurden mit einer Auflösung von 640x480 Pixeln gerechnet.)
File translated from TEX by TTH, version 1.0.
Zurück zu Fraktale und Chemie
Zurück zur Startseite
Kai Schröder, 29.11.2000 









