Saturation effects in diving, the Model ZH-L16,
operation of dive computers
by Kai Schröder
and Steffen Reith
translated by Achim Lohse
and Kai Schröder
Stand> December 14th, 2000
deutsche Version
versione italiana
The following explanations and examples are presented conscientiously to the best
of our knowledge. However, we can't guarantee the complete absence of errors, and
would welcome being informed of any you find, so we can fix them. We would also
point out especially that
Tausim
is not meant to be used for planning real dives, only to explore dive scenarios
theoretically!
Content
1 A couple of preliminary explanations
2 Saturation and desaturation of tissues
3 The Model ZH-L16
4 A short commentary on decompression tables
5 Flying after diving
6 The limits of the model
7 Breathing nitrox instead of air
7.1 maximum operation depth (MOD)
7.2 optimal oxygen proportion in the breathing mixture (Best Mix)
7.3 equivalent air depth (EAD)
8 Operation of dive computers - an algorithmic survey
8.1 an overview
8.2 calculation of the inert gas content
8.3 determination of the maximum tolerable supersaturation
9 A short note on calculation of air consumption
10 A few closing comments
11 Literature, links
1. A couple of preliminary explanations
Air consists of approximately 21% oxygen (O2) and 78% nitrogen (N2) by
volume. The remaining 1% consists of carbon monoxide (CO), carbon dioxide (CO2),
various nitrogen oxides and noble gases (Helium, Neon, Argon). Except for oxygen,
all of these components are relatively non-reactive - practically they do not interact
chemically with other molecules - and are thus grouped as "inert gases". When N2
is mentioned below, all of the inert gases should be meant, strictly speaking.
However, since the proportion of the remaining gases (CO, CO2, nitrogen oxides,
noble gases) in air is so slight, they are of no practical importance. Therefore
saturation calculations allways simply use a volume of 79% N2.
When diving with other gas mixtures, such as Trimix (O2, N2,
Helium) or Heliox (O2, Helium) instead of compressed air, the Helium naturally
has to be entered into the calculation!
The Swiss medical doctor Albert A. Bühlmann developed the Model
ZH-L16 to calculate saturation processes in the human body, and published his work
in the book "Tauchmedizin", - Barotrauma, Gasembolie, Dekompression,
Dekompressionskrankheit, Dekompressionscomputer -, published by
Springer Verlag,
- a reworked and expanded edition appeared in 1995, an English translation of the 4th edition
of the book is in preparation for publication. In contrast to the older model which specified
16 tissue compartments, the newer Model ZH-L8ADT uses only 8, but takes into consideration the
effects of temperature and work (breathing frequency) under water, as well as microbubble
formation. All Aladin dive computers currently produced by the firm Uwatec utilize this new
ZH-L8ADT model. Unfortunately, the Model
ZH-L8ADT is described only very superficially in the latest edition of "Tauchmedizin",
without any quantification of parameters! :-( This refusal to reveal in detail the operating
principles of dive computers is a trend observable with all manufacturers known to us, and is
a regretable development for diving safety, as it prevents discussion and independent
verification of their effectiveness.
2. Saturation and desaturation of tissues
Let's say we've been at sea level for several days already - say in Northern Italy. :-)
The different tissues of our body will then be saturated at pressure of one atmosphere
or 1 bar (fluctuations of a few millibars are insignificant here). This means absorption
and off-gassing of nitrogen is balanced. When we dive, the ambient pressure rises sharply
- much more than if we descended from the mountains into a valley - by roughly one
atmosphere per 10m (33 feet) of depth.
As soon as we submerge, our tissues become undersaturated in relation to nitrogen.
Since we're breathing at ambient pressure, a partial pressure difference exists between
the nitrogen component of the air in our lungs, and that in our tissues. Therefore more
nitrogen is absorbed from the blood into the tissues than is released into the blood to
be exhaled. This is how the tissues achieve saturation. The speed of saturation of a
given tissue is proportionate to the size of its blood supply.
The inert gases are physically dissolved in the blood and the tissues. The amount of
absorption at a given pressure varies with temperature, with colder temperature increasing
the amount of absorption. Nitrogen is absorbed more readily by fat than by water and blood.
Bodily circulation is divided into several parallel systems. The blood supply of the
various tissues and organs varies considerably, depending on their weight and working
status. The blood supply of the brain, spine, kidneys and liver are constant, and are
not affected by muscular activity. However, blood supply to the working muscles is
increased sharply (together with nitrogen absorption) with expansion of the blood vessels.
At the same time, circulation of the skin and the underlying fatty tissues increases in
order to better dissipate the resulting heat. But since water is a much better heat
conductor than air, this last mechanism is hardly a factor in diving. Skin circulation
may even be lower under water than in high air temperatures on land.
If we were to stay at depth long enough (for example doing saturation diving on an
off-shore rig), all of our tissues would eventually reach saturation relative to the
ambient pressure.
Then, when we surface, everything is reversed - the ambient pressure is reduced, and
our tissues are now supersaturated with nitrogen. Consequently (since the partial
pressure of N2 in the lungs is now lower than that in the tissues) nitrogen
is released from the blood into the lungs. If we've followed procedure in our ascent,
our tissues will be properly desaturated after a certain period of time at the surface.
Problems arise when the ascent is too rapid for the nitrogen to off-gas sufficiently.
Then, besides the very small microbubbles (which are practically unavoidable) larger
bubbles can be formed, which can lodge in the joints, clog arteries, or pinch nerves
in the spine. This is when the familiar symptoms of decompression sickness arise.
The
process of saturation and desaturation during a dive
can be calculated and displayed graphically with the program
Tausim.
3. The model ZH-L16
The Swiss medical doctor Albert A. Bühlmann has established, by means of many
hyperbaric chamber experiments with volunteers, how much supersaturation the
individual tissues (compartments) can tolerate without injury. He expresses the
relationship through the following equation:
|
pamb. tol. = (pt. i.g. - a) ·b |
| (1)
|
or
|
pt. tol. i.g. = (pamb / b) + a |
| (2)
|
pamb. tol. - the ambient pressure tolerated by the tissue
pt. i.g. - the pressure of the inert gas in the tissue
pt. tol. i.g. - tolerated (excess)pressure of the inert gases in the tissues
pamb - current ambient pressure
a, b - parameters of the model ZH-L16 for each tissue
a depends on the measure unit of pressure used, while b lacks dimension, and represents
the steepness of the relationship between the ambient pressure pamb. and the
pressure of inert gas in the tissue pt. i.g. The first equation shows which
lower ambient pressure pamb. tol. will still be tolerated at the actual pressure
of inert gas in the tissues pt. i.g. The lower equation shows which level of
supersaturation pt. tol. i.g. can be tolerated at a given ambient pressure
pamb for a given tissue.
The rate of change (de)saturation takes place depends on the gradient of inert gas
pressure in the lung and in the tissues. According to Bühlmann, the saturation
and desaturation of the various compartments can be calculated as follows:
|
pt. i.g. (tE) = pt. i.g. (t0) + [pI i.g. - pt. i.g. (t0)] ·[1 - 2-tE / t1/2] |
| (3)
|
pt. i.g. (t0) - pressure of inert gas in the tissue at start of exposure
pt. i.g. (tE) - pressure of inert gas in the tissue at end of exposure
pI i.g. - pressure of inert gas in the breathing mix
tE - duration of exposure in minutes
t1/2 - half-time in minutes
Equation (3) is valid only for constant pressure, i.e. remaining the whole time
at the same depth during diving. In practice this will hold only in the scarcest
cases. Normally many changes in depth do occur. To treat this behaviour it's
common use to split the profile into many small parts, presuming that the whole
time of these bits is remained at the same depth.
A more elegant solution of the above is the following equation (4) by
Schreiner. Here it is presumed, that descent and ascent take place
with constant velocity:
|
pt. i.g. (tE) = pI i.g. + r(tE - 1/k)
- [pI i.g. - pt. i.g. (t0) - r/k] ·
e-k · tE |
| (4)
|
pt. i.g. (t0) - pressure of inert gas in the tissue at start of exposure
pt. i.g. (tE) - pressure of inert gas in the tissue at end of exposure
pI i.g. - pressure of inert gas in the breathing mix
tE - duration of exposure in minutes
k - half-time-constant in minutes (ln 2 / t1/2)
r - rate of change in inspired gas pressure with change in ambient pressure (this means rate
of de-/ascent multiplied by inert gas fraction)
For r = 0 the Schreiner equation reduces to equation
(3), which therefore is a special case of (4).
Equation (3) can be transformed so as to directly calculate the no-decompression time
(meaning the time underwater after which one can still ascend immediately to the surface):
|
no-decompression time = -t1/2 ·log2 [ |
pI i.g. - pt.tol. i.g. (tE)
pI i.g. - pt. i.g. (t0)
|
] |
| (5)
|
pt.tol. i.g. (tE) - maximum tolerable excess pressure of inert gas
of the leading tissue at the surface
No-decompression time is the time one can remain at depth without having to decompress
while surfacing. The tissues can only have saturated so much, that a rapid ascent to the
surface will not exceed the maximum tolerable pressures of the leading tissue.
Leading tissue: that tissue which currently tolerates the lowest ambient pressure
without symptoms. The other tissues (compartments) could tolerate even further ascent
without showing symptoms of decompression sickness. The leading tissue can tolerate no
further decrease in the ambient pressure without risking the occurrence of symptoms of
decompression sickness.
Saturation and desaturation proceed exponentially. The measure for it is the
so-called half-time, which represents the time it takes for the initial value
- in this case, the degree of saturation - to halve or double.
The model ZH-L16 stipulates that the rate of blood
supply to a tissue (compartment) determines the half-time. The absorption of nitrogen
and the rate of blood supply then determine the amount of partial pressure of inert gas
the compartment can tolerate.
Compartments with short half-times tolerate greater excess pressure of inert gas
than the slow compartments.
The order of the compartments (tissues) in the model is as follows:
| Number 1 - 4 |
fast tissues: central nervous system, spine |
| Number 5 - 11 |
the skin (overlapping) |
| Number 9 - 12 |
the muscles (overlapping) |
| Number 13 - 16 |
slow tissues: limbs, with ligaments, cartilege, and bones (overlapping) |
("overlapping" means that the slowest tissue of the group has a longer half-time than
the fastest tissue of the adjacent slower group shown as overlapping)
| compartment |
[min] |
b |
a (theoretical) |
a (table) |
a (computer) |
| 1 |
4,0 |
0,5050 |
1,2599 |
1,2599 |
1,2599 |
| 2 |
8,0 |
0,6514 |
1,0000 |
1,0000 |
1,0000 |
| 3 |
12,5 |
0,7222 |
0,8618 |
0,8618 |
0,8618 |
| 4 |
18,5 |
0,7825 |
0,7562 |
0,7562 |
0,7562 |
| 5 |
27,0 |
0,8126 |
0,6667 |
0,6667 |
0,6200 |
| 6 |
38,3 |
0,8434 |
0,5933 |
0,5600 |
0,5043 |
| 7 |
54,3 |
0,8693 |
0,5282 |
0,4947 |
0,4410 |
| 8 |
77,0 |
0,8910 |
0,4710 |
0,4500 |
0,4000 |
| 9 |
109,0 |
0,9092 |
0,4187 |
0,4187 |
0,3750 |
| 10 |
146,0 |
0,9222 |
0,3798 |
0,3798 |
0,3500 |
| 11 |
187,0 |
0,9319 |
0,3497 |
0,3497 |
0,3295 |
| 12 |
239,0 |
0,9403 |
0,3223 |
0,3223 |
0,3065 |
| 13 |
305,0 |
0,9477 |
0,2971 |
0,2850 |
0,2835 |
| 14 |
390,0 |
0,9544 |
0,2737 |
0,2737 |
0,2610 |
| 15 |
498,0 |
0,9602 |
0,2523 |
0,2523 |
0,2480 |
| 16 |
635,0 |
0,9653 |
0,2327 |
0,2327 |
0,2327 |
Coefficients of the model ZH-L16 for
Note : The a parameter depends on the measure unit of pressure. Here we used
the unit bar for pressure as is in the original book by Bühlmann.
(Dive tables use additions for time, depth, and initial partial pressure of nitrogen,
while dive computers have the real ambient pressure and the actual dive profile at
their disposal. Therefore Bühlmann provides two modifications for the parameters, in
addition to the theoretical model.)
On longer dives with higher saturation of the tissues, the decompression profile is
always determined by the compartment with the longest half-time. With partial
saturation, the maximum allowable partial pressure shifts from the tissues with
shorter half-times to those with longer ones. The more compartments are considered
in a model, the more accurately the required decompression can be determined (and thus
the individual deco stops can be minimized). The tissue which determines what partial
pressure of inert gas is still tolerable is designated the leading tissue.
The ideal situation consists of a continuous decompression. Instead of spending a set
time at specific depths (such as 30ft, 20ft, 10ft), the diver would ascend in accord
with the increasing tolerance of his leading tissue. But this is practically impossible,
and so decompression must take place at certain - arbitrarily chosen - depth stages.
The diver must remain at a given depth or range of depth, respectively, until it is
safe to ascend to the next one.
It often happens that the leading tissue changes during the ascent or during a deco
stop. In this case, a slower compartment becomes the leading one. Thus a dive computer
may at first show no need for a decompression stop, then demand one later on during
the ascent. While irritating, this is not a sign of a defect in the computer!
(
example of this phenomenon
)
A large number of compartments with various half-times must be considered in order
to minimize both the risks in decompression and the time required for deco stops
both for dives of only a few minutes' duration and for those of several days
(in the case of industrial divers).
4. A short note on decompression tables
The "Deco '92" (in the meantime the successor "Deco 2000" is available)
dive tables commonly used in Germany (in Europe?) were developed
by Dr. Max Hahn. Such tables naturally can't reflect the real dive profile. As Max
Hahn has remarked, the "Deco '92" tables assume descent and ascent rates of 33 feet
per minute. The waiting periods at required decompression stops must be spent
stationary at the stipulated depths. This procedure is easy to carry out with the help
of a watch, compared to trying to factor the effects of a gradual ascent into the
decompression stops. Since one doesn't usually spend the entire "bottom time" at the
bottom, taking instead some time to reach bottom, and then gradually rising slowly
in the course of the dive, the tissues are not as saturated in the real dive profile
as determined by the set procedures of the dive table. Because of this there is always
a safety buffer in using the tables (assuming one has used them correctly ! :-) ) !
Note : The above said is valid for all dive tables, not only for "Deco '92" or
its successor "Deco 2000" !
Because of the conservative rounding off of dive tables, a dive computer will always
allow a longer no-decompression time and shorter decompression stops. However, this
doesn't mean that diving with the computer entails greater risk.
Why do the "Deco '92" tables start only with a depth of 30 feet? At 30 feet, or even
40 feet no-decompression stops are required. Only when one has spent more than 64
minutes at 50 feet is a three minute stop at 10 feet required (the table gives a no
decompression time of 72 minutes). Certainly scarcely a recreational diver would (or could)
spend so much time at this depth. The dive computer reports an infinite no
decompression time at these depths. Is the no-decompression time above 10 feet really
endless ?
No, not necessarily. The saturation equation simply can't calculate the no-decompression
time above 22 feet - the argument of the logarithm becomes negative (see equation
(5)), which isn't allowed. However, this problem is negated by
experimental evidence that even fully saturated tissues can tolerate abrupt surfacing
from this depth due to the fact, that the tolerated ambient excess pressure doesn't fall short.
In any case, the tables are formulated in 10 feet increments, and the first depth for
which no-decompression time can be calculated with them is that of 30 feet.
5. Flying after diving
In flying we confront a situation where the ambient pressure drops rapidly after
the airplane takes off. If the allowable partial pressure in any of the tissues
is overstepped by this drop in pressure, symptoms of decompression sickness are
likely to arise.
To avoid this situation, the "do not fly" time must be observed after diving.
Most dive computers calculate and display this waiting period, which may correspond
to the period required for complete desaturation. However, there is considerable
variation in the "do not fly" period calculated by different dive computers for
the same dive profile. This raises the question of how this waiting period is
calculated, and why significant differences are found between the calculations
of different dive computers.
According to Bühlmann, the "do not fly" period is the time span after which
even the slowest tissue has decompressed sufficiently that even an instantaneous
drop in ambient pressure to a specific level will not exceed the partial pressure
tolerance of this tissue
- quite a mouthful ! :-) -
This "specific level" in question is the usual cabin pressure of a commercial
airliner, equivalent to atmospheric pressure at an altitude of 6000 feet. However,
in an emergency, this pressure can drop to ambient levels, and therefore an altitude
of 13000 feet may be used to provide a further safety factor. The Aladin dive
computers go even further and use an altitude of 15000 feet. But . . .
To further confuse you (or make you think !) here's a small example: after a given
dive, the Aladin Air X showed a "do not fly" time of 9 hours, while my buddy's
Scubapro DC12 showed 24 hours. Tausim, using
the same dive profile, calculated a "do not fly" period of 17 hours. (But
when a cabin pressure of 6000 feet was stipulated, this dropped to only 13 minutes !)
What's the right answer ?
To deepen the confusion even more, it must be noted that the 17 hours "do not fly"
time generated by Tausim is not accurate either
- not even within the framework of the ZH-L16 model ! This
is due to the fact that with longer and/or deeper dive simulations the slower tissues show
negative values for the argument of the logarithm due to mathematical limitations of the
Bühlmann model. Since negative arguments for the algorithm are not allowed, these
tissues can't be used in the calculation of the "do not fly" time, and so it is determined
using the slowest tissue that still shows a positive value for the argument of the logarithm.
This means that the real "do not fly" time is longer than that shown by
Tausim.
Because of this, one must take as a given, on longer dives, that the actual "do not
fly" time is longer than that shown (because the slower tissues have saturated further
on such a dive). And this is why Tausim also
reports, when giving the "do not fly" time, which tissues were included in the
calculation. Whenever less than 16 tissues produce a positive argument for the logarithm,
then the real "do not fly" time is significantly greater than shown.
Yet we previously mentioned that the Aladin dive computer uses a cabin pressure of
15000 feet for extra safety. How can its "do not fly" time be so much shorter at
9 hours, when one would expect it to be longer compared to times calculated on a
cabin pressure of 13000 feet ? It's due to the fact that Aladin dive computers use
a mid-range tissue instead of the slowest tissue for the calculation.
Experience has shown that the symptoms of decompression sickness produced by flying
to soon occur (predominantly or only ???) in the mid-range (for half-time) tissues.
Thus Uwatec can advertise seemingly more safety with its "do not fly" calculations
based on a 15000 feet cabin pressure, while keeping the "do not fly" time quite short.
Since the ZH-L8ADT model is safer (more conservative,
especially for repetitive dives) than the ZH-L16 model
according to Uwatec, one would hardly suspect that the "do not fly" time calculated
by the Aladin dive computers might be a bit skimpy! Unfortunately, there is no
indication in the user's manual of the Aladin dive computer of the actual compartments
used in this calculation. :-(
How does the Scubapro DC12 deal with this situation ? It simply gives the time to
complete decompression as the "do not fly" time. Since in using the
ZH-L16 model practically every dive profile results in
unuseable data for the 4 slowest tissues, the actual "do not fly" time is
always longer than that produced by Tausim.
Simply using the time to complete desaturation as the
"do not fly" time assures that one is always safe ! However, it also means that the
"do not fly" time resulting from two, three - or sometimes even more ! - dives per day
over a period of several days can significantly exceed 24 hours. How many divers would
choose to give up diving during the last two days of a week-long dive vacation ?
How do other dive computer manufacturers handle this problem ? On this subject
they either plead "trade secrecy" or offer such useless descriptions as
"modified Haldane algorithm", without providing any details of the
"modification" (in principle the Bühlmann model is a haldanian
model, too. - May be, all the different dive computers use the Bühlmann
model . . . ??? :-) ). This is the dark side of dive computers, which constitutes
a significant risk for divers. :-(
Max Hahn has stated that the "do not fly" times of some dive computers are more a
product of the influence of strict US product liability considerations informed by
the position of the US-dominated Undersea and Hyperbaric Medical Society (UHMS) than
of experimental data. According to Hahn, the earlier "do not fly" periods of
Bühlmann are too short. A reliable rule of thumb for safe "do not fly" times
would be to take 60% of the "do not fly" time shown by the DC12/TRAC.
According to Hahn, the "total decompression" time (ie. all tissues clear of N2
excess pressure) calculated by various dive computers is equally unreliable, because
it is dependent on the number of bits used to store a value by each computer. Careful
review of all the experimental data led Max Hahn to come up with the rule : To fly you
must be nitrogen "clean".
6. The limits of the model
At the beginning of this article we assumed to be at sea level in northern Italy.
Because the harpooners have shot most of the fishes in the Mediterranean Sea we
decide to make our next scuba dive in a clear and unspoiled alpine lake. :-)
No problem, our dive computer has a so-called "mountain lake" program on its
disposal !
Our body is saturated with nitrogen corresponding to sea level, when we start our
tour to the mountain lake. When we now do ascend while driving, it's a similar
situation as surfacing at the end of a dive - the ambient pressure lowers faster
than off-gassing of the body can take place.
Let's further assume, that the lake is located at an altitude of 4500 feet and we
needed 8 hours to reach it. Using the model ZH-L16
now shows an interesting effect : we are still standing on the beach and haven't
entered water so far - and now all 16 compartments can be used for the
decompression calculation, that means, the slowest tissue can contribute ! We
come up with a computed "do not fly" time of 5 h 10 min, and the desaturation time
is more than 33 hours ! So, after a period of 5 hours we would be to fly again -
but so far we haven't dived, only went by car uphill !!! :-) No one would say, that
this "do not fly" time is realistic and trustworthy !
Now we do our dive for about 20 minutes at a depth of 30 feet and surface slowly.
Even now all compartments contribute to the decompression calculation - but now
the desaturation time is more than four times longer than the "do not fly" time
when applying a pressure according to 13000 feet ! When we take the desaturation time
as the "do not fly" time, it's much more worse !
This mountain lake example was calculated under assumption that saturation and
desaturation take place with the same rate, i.e. adjusting the half-times
to be symmetrical during off-gassing, which isn't realistic. When taking into
account longer half-times during off-gassing (more conservative) the "do not fly"
time will be even more greater.
Here the limits of the model become evident. But one should not take for
granted, that such a rudimentary model is able to reflect all phenomenons of
de/saturation in the human body, of course. Normally, the Bühlmann model
serves well !
Result :
Without thinking never believe to all the dive computer will tell you !
Especially in the case of short or no "do not fly" time, which is pleasant for
the diver. It's ours to voluntary lengthen it for our own safety. Best behaviour
is, not to dive on the last day before flying back from a diving vacation.
It's better to drop a dive than to be delivered in a hyperbaric chamber next
day !
7. Breathing nitrox instead of air
We call a breathing gas "nitrox", when its O2 fraction is greater and
its N2 fraction is less than in air (in principle air is a nitrox
mix, too - with 21% O2 and 79% N2). The nitrogen is liable
for decompression sickness DCS (and for deep intoxication ). If the
nitrogen fraction in the breathing gas is lowered, the following advantages do
arise :
- longer no-stop time
- shorter decostops
- when using a non-nitrox dive computer more safety as a whole
- a shorter surface interval
- less weariness after diving
The disadvantage is, that the maximum allowed depth is less than diving with air.
This is due to the fact, that the O2 fraction now is higher and so the
critical O2 partial pressure, when O2 becomes toxic, is
reached faster. Filling a tank with nitrox necessitates a greater apparative expense,
wherefore nitrox is more expensive than air. Finally, before each dive the O2
fraction in the breathing gas has to be checked and input into the computer (in the
case it supports nitrox).
The normally used nitrox mixes are NOAA Nitrox I
(32% O2, 68% N2) and NOAA Nitrox II
(36% O2, 64% N2, besides there do exist some more "standard" mixes.
Although air is a nitrox mix in principle, some additional facts have to be
considered (which were "omitted" in our air scuba lessons :-) ).
7.1 maximum operation depth (MOD)
Though oxygen is of vital importance, it will become (life)threatening when breathed
in too high concentration. The maximum operation depth (MOD) is reached, when the
partial pressure of O2 reaches its upper limit. This critical pressure is
1.6 bar in warm water and without exertion, in cold water and/or exertion this
value lowers to 1.4 bar. Therefore, dependent on the used nitrox mix the MOD varies
and this is why it's of overall importance to check the oxygen partial pressure
before diving. The relevant law in this case is Dalton's law: The total
pressure is the sum of the partial pressures of each of the components of the gas.
In our case this means: The partial pressure of one of the gas components proves to
be the total pressure multiplied by the fraction of this component in the gas mix.
with the meaning of the symbols as follows:
p - total pressure
fO2 - O2 fraction in breathing gas
pO2 - O2 partial pressure in breathing gas
To calculate the MOD, (6) has to be transformed:
For pO2 the wanted maximum allowed oxygen partial pressure has
to be given (1.4 bar or 1.6 bar, respectively) and for fO2 one
has to input the oxygen fraction of the nitrox mix to be used (for example 0.36 for
Nitrox II). The result is the maximum operation pressure (MOP), which has to be
converted to depth:
|
MOD = (MOP - 1 bar) · 33 ft/bar |
| (8)
|
Using air we get a depth of about 218 feet, for Nitrox I the MOD is about
132 feet, and in the case of Nitrox II it's about 112 feet, when we set the critical
O2 partial pressure to 1.6 bar.
7.2 optimal oxygen proportion in the breathing mixture (Best Mix)
For a long no-stop time the nitrogen fraction has to be as low as possible, corresponding
with a high oxygen fraction. According to the wanted MOD, the partial pressure of O2
must not be exceeded. The so-called "Best Mix" then is the oxygen fraction at MOD,
where the maximum oxygen partial pressure is reached. To get the "Best Mix", we have
to transform (6) again:
p now is the pressure at MOD
7.3 equivalent air depth (EAD)
Using air as breathing gas at given depth the partial pressure of nitrogen is greater
than using nitrox with a lower N2 fraction. If we take a given N2
partial pressure reference instead, we get a lower depth with air as breathing gas than
if using nitrox as breathing gas.
This fact is important if we want to do a nitrox dive but our deco table is
calculated for air - which should be the normal case (otherwise one would have to calculate
a deco table for each nitrox mix). After calculating the equivalent air depth (EAD)
it is possible to plan a nitrox dive with an ordinary air-based deco table. The formula to be
used in this case is as follows:
|
EAP = | fN2(nitrox)
fN2(air) | · p |
| (10)
|
EAP (equivalent air pressure) is the equivalent total pressure subsequent to be transformed
into the EAD:
|
EAD = (EAP - 1 bar) · 33 ft/bar |
| (11)
|
Due to the fact that the N2 fraction in air is always greater than in a
nitrox mix the ratio fN2(nitrox) / fN2(air)
is always less than 1. Therefore the EAD is always less than the real depth.
In most books and training manuals (10) is given in this simple form:
This is "correct", of course, but sometimes (in the German diving magazine
"Divemaster" unfortunately more often) misprints do occur. If the value
0.79 is printed instead of fN2(air) or - more worse - the digits
were permuted to 0.97 - as happened in "Divemaster", issue 1/98, pp. 37 and 38 !
- it's not clear on first sight why 0.79 or one comes up with totally wrong findings !
Therefore, for a better understanding the formula should always be given in the form of (10).
The model ZH-L16 is without limitation applicable for nitrox
as breathing gas, too.
8. Operation of dive computers - an algorithmic survey
In this section an algorithmic survey concerning the decompression model
ZH-L16 is given. A more detailed description and derivation
of this model can be found in Bühlmann. More information
about the often used Haldane-like simulation models is found in
The Physiology and Medicine of Diving
for example.
At the beginning of each section a brief recapitulation of the known contexts
is given. The used algorithms are presented in a PASCAL-like pseudo code,
because we think that this is the best manner to do.
8.1 A survey
The model ZH-L16 can roughly be divided into two
different domains.
- Calculation - in the following the term "calculation" is used
as a synonym for simulation/approximation - of the inert gas loading of the
tissues.
- Determination of the maximum tolerated excess pressure of the inert gases
in the tissues.
8.2 Calculation of the inert gas loadings
If there exists a gradient between the inert gas pressure in the lungs and
the inert gas pressure in the tissues a pressure equalization will take place.
It is presumed that for each different tissue (compartment) there is a
characteristic velocity of saturation and desaturation with inert gases.
(Therefore it is often spoken of "fast" and "slow" tissues.)
Furthermore it is assumed, that there is no pressure equalization
between compartments with different inert gas pressure in the model
ZH-L16.
The phenomenon of this pressure equalization is easily described by a linear
differential equation which solution is an exponential function:
|
pt. i.g. (tE) = pt. i.g. (t0) + [pI i.g. - pt. i.g. (t0)] ·[1 - 2-tE / t1/2] |
| (3)
|
with the following meanings of the used symbols:
pt. i.g. (t0) - inert gas pressure at beginning of exposition
pt. i.g. (tE) - inert gas pressure at end of exposition
pI i.g. - inert gas pressure in breathing gas
tE - time of exposition in minutes
t1/2 - half-time in minutes
Although the above equation is valid only for a constant inert gas excess pressure
(and therefore for a constant depth), it can be used to simulate whatever
dive profile is given. The idea, often used in numerical mathematics
techniques, is easy to understand. If we are able to measure the pressure in
very short cycles, its value will not differ (much) and we can calculate the
inert gas pressure with this equation. If we apply this method sufficiently
often we get a good approximation of the real course of inert gas pressure.
The shorter the time between two measurements the better the approximation
will become. Vivid this means that the dive profile is approximated by a huge
number of steps and for each step equation (3) has to be used (see picture).
After this short description of the theoretical background for the calculation
of the inert gas loadings of the tissues we can proceed to the algorithm
itself. We presume that the diver is fully saturated with the inert gases at
the beginning of the dive.
Complete simulation of the dive:
FORALL (tissue Ti) DO
FORALL (inert gas Ij) DO
/* If for example Ij = N2, then the partial pressure
of N2 = 0.79 bar (in case breathing gas is air) */
set pressure for Ij in Ti to the partial pressure
of inert gas Ij in the present breathing gas;
Calculate the tolerance coefficients a and b for tissue Ti from
the half-times of inert gas Ij;
END FORALL;
END FORALL;
WHILE (simulation is going on) DO
Measure present environmental pressure;
Check ascent velocity by means of changes in the environmental pressure;
FORALL (tissue Ti) DO
Calculate new loadings of all inert gases for Ti;
IF (no decompression stop necessary for tissue) THEN
Calculate no-stop time for tissue Ti;
ELSE
Calculate next depth for decompression stop;
END IF
END FORALL;
IF (all tissues in no-stop time) THEN
Calculate minimum of all no-stop times (shortest no-stop time is relevant for diver);
ELSE
Calculate depth and duration for first (deepest) decompression stop;
END IF;
Wait a small interval Dt;
END WHILE.
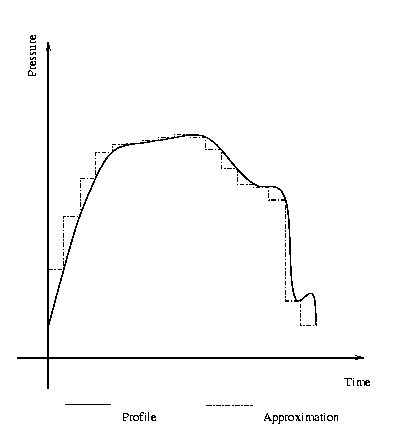
Example for the approximation of a pressure profile
The calculation of the tolerance parameters a and b for each half-time or
tissue combination and inert gas combination, respectively, is performed
in an algorithmic way or the parameters are stored in a table in the program.
In the book by Bühlmann both possibilities
are described. The formulae to obtain the parameters a and b for the inert
gases N2 and He are simple ones. Simultaneously the parameters are
given in tables for a suitable spectrum of half-times for Nitrogen and
Helium. The layout of these tables is appropriate for the direct use in dive
computers. (For Nitrogen three different sets for the parameter a are
given, for Helium there is no differentiation.)
Calculation of the parameters a and b for
tN21/2:
a := 2.0bar (tN21/2)-1/3;
b := 1.005 - (tN21/2)-1/2;
A short remark on when the simulation can be put to an end. When the diver
reaches the surface the tissues are still partly saturated with the breathed
inert gases. This partial saturation of the tissues roughly corresponds with
the repetitive dive groups known from the slates. Therefore the
simulation must not be finished when reaching the surface. Instead it is
assumed, that the diver "continues to dive" at surface pressure. So
the progress of desaturation at the surface is simulated. The simulation can
be finished, when it is "sure" that all the tissues are desaturated
in this manner, that the do-not-fly time has diminished to zero. As mentioned
before, dive computers of different manufacturers do use different criterias
for the calculation of the do-not-fly time.
Dive computer measure the ambient pressure very accurately with their sensors.
Using a dive simulation program like Tausim
the pressure data are calculated directly from the given profile. It must be
considered that the surface pressure depends on the height above sealevel, of course.
After passing by of Dt the new inert gas loading
of each tissue is calculated with formula 3. If
Dt is sufficient small the approximation is
well done to reflect reality. You can imagine, too, that each dive meets a
multi-level dive with many very short levels, and it's assumed that during
this time the depth (more precisely, the ambient pressure) is constant.
To achieve an exact simulation, a reduced emission of inert gases by means
of microbubbles in the lungs have to be taken into consideration. This
effect, known as intrapulmonary right-left-shunt, is not taken
into account within the model ZH-L16. Only
the improved model ZH-L8ADT includes this
feature. Unfortunately, this technique isn't described in full in the book
by Bühlmann.
According to the model ZH-L16 now the new
inert gas loading in the body tissues is calculated. To do this formula
3 is used, as mentioned above.
Calculate the new loading of all inert gases for Ti:
FORALL (inert gas Ij) DO
calculate current inert gas pressure pIj in the
breathing gas;
calculate new loading of inert gas Ij in tissue Ti
with half-time tIj1/2 according to
3
END FORALL;
8.3 determination of the maximum tolerable supersaturation
It's possible to compute for each tissue and for each inert gas a still
tolerated ambient pressure, which isn't allowed to fall below. Bühlmann
describes this correlation simply as follows:
|
pamb. tol. = (pt. i.g. - a) ·b |
| (1)
|
or
|
pt. tol. i.g. = (pamb / b) + a |
| (2)
|
with
pamb. tol. - still tolerated excess pressure by the tissue
pt. i.g. - inert gas pressure in the tissue
pt. tol. i.g. - still tolerated (excess) pressure in the tissue
pamb - current ambient pressure
a, b - parameter of the model ZH-L16 for each tissue
Now the so-called "no-stop time" is that time, the diver (or the tissue) is
allowed to remain at the current pressure, until the tissues are saturated
to an extent, that the still tolerated inert gas pressure (that means, the
pressure at the surface) is reached. Staying for a more prolonged period at this
depth the tissues will saturate even more, so that at the surface a higher
partial pressure of the inert gases is reached than is tolerable (by the
tissues). That means, decompression sickness symptoms are likely to occur.
In similar action decompression stops are to be calculated. If a tissue is
outside no-stop time, the next depth to stop is given by that (less)
pressure to which ascending is allowed without falling below only just
the tolerated partial pressure of the respective tissue. The deco stage
then is the maximum of all such pressures for the tissues. Further ascending
would get at least one tissue to be supersaturated, which would lead to a
higher risk for the occurence of DCS at least. In practice the corresponding
depths to stop are rounded to multiples of 10 ft. By this an additional
safety is gained and on the other side it would be very difficult to keep
deco stops with shorter distances.
Decompression calculation can be performed without explicit deco stops. In
this case the diver has to stay exactly at that ambient pressure which is
tolerable only just. This continuous decompressioning is not or, at least,
only extremely difficult to perform for a scuba diver and who wants to
claim that he/she is able to do this ? At waves this variant would be
impossible to perform, anyway.
A simple conversion of formula (3) gives:
|
no-stop time = -t1/2 ·log2 [ |
pI i.g. - pt.tol. i.g. (tE)
pI i.g. - pt. i.g. (t0)
|
] |
| (5)
|
pt.tol. i.g. (tE) - maximum tolerated inert gas excess pressure
of the leading tissue at surface
Well-versed people in the field of mathematics at once see, that there
are cases in which formula (5) gives no solution. In case the fraction
is less or equal to 0, the logarithm cannot be computed. Now one
can examine, when this will happen. For the sake of simplicity we will
give some hints here.
When diving in shallow depths it's possible, that the ambient pressure
of the inert gases even at saturation of the tissues is less than the
maximum tolerated pressure at the surface. That means, if a tissue stays
endless at such a depth, and therefore is completely saturated, surfacing
is allowed. The no-stop time in this case is endless. This is valid at
least for the model ZH-L16. Whether there
do exist other phenomenons, which demand decompression stops in this case
we don't know (please tell us, if you know some facts about this topic).
Another case can be thought of: if a diver has to perform some decompression
stops and stays at a depth in which further saturation takes place, that
means the inert gas partial pressure inside ths tissues is less than the
inert gas pressure in the breathing gas, the diver never can come back to
a positive no-stop time. In other words: the diver not only has to perform
decompression stops but these stops will become longer and/or deeper.
Calculate no-stop time for tissue Ti:
BEGIN
/* see formula (1) */
calculate the only just tolerated partial pressure of the inert gas
for this tissue:
calculate the current partial pressure of the inert gas in the breathing gas;
calculate no-stop time for the tissue using formula (4);
END;
The algorithm for Calculate next decompresion stage is easily
obtained with the above mentioned from a generalized no-stop time
calculation. In practice it's good use to develop such a generalized
calculation and to treat the no-stop time calculation as a special
case (ascent to surface).
9. A short note on calculation of air consumption
Meanwhile one can purchase dive computers, which take into account the
air consumption in their calculations and present the remaining bottom time (RBT)
in the display. This is useful especially in the need of more than one deco stop
at different depths. Because the dive computer knows the real air consumption
(air consumption volume (ACV) isn't constant during diving !), it is able to
determine the RBT with sufficient precision. This value is always more precise
than a calculation "by hand" with supposed ACV. To be able to calculate the RBT
the dive computer has to know the initial air volume and the drop in pressure at
the first stage has to be measured very accurately.
Nevertheless, no dive computer requires an input of the tank volume. This could
become even dangerous, if one dives with different sized tanks and one forgets
to change the tank volume in the computer (what would happen without fail sooner
or later) ! How is the dive computer able to correctly calculate the RBT, when it
doesn't knows the tank volume ?
That's not as difficult as it seems to be, but takes for granted a very accurate
pressure measuring at the first stage, what is no longer a technical problem today.
The first output of the RBT takes place after some minutes only. During the first
minutes of a dive the drop in pressure as against the initial tank pressure is only
slight and the outputted RBT is only a very rough estimation. This doesn't matter,
because the tank is full at this time. The more air is consumed during the dive
the less the relative error in the difference between initial pressure and
momentary pressure will become and therefore the extrapolation of the RBT becomes
more accurate.
At high pressures it's not possible to treat air as an ideal gas (no
interactions of the molecules or atoms, respectively, with each other). In this
case a sufficient exact equation of state for air must be used.
Here, too, the manufacturers don't want to publish any details. When I (Kai)
asked Uwatec at the boot'97 fair, at once I was suspected to be an industry spy ! :-)
(The friendly man stated, he had told me too much, when he explained to me the
technique of the approximation of the RBT. And now he could not tell me the
equation of state used by Uwatec, even more ! "What do you think, how many
industry spies are strolling around here !?") Since some time on the
Uwatec Homepage, "Technical" section, you
can find the statement, that they use the van der Waals equation
of state.
In comparison with the ideal gas law, the van der Waals equation of
state for real gases is an improvement. Here the particles are treated as hard
spheres, which attract themselves when coming close together. At least a
qualitative description of a real gas is possible with this
equation of state. Engineers often use so-called empirical
equations of state. These equations of state often show a lack of any physical
significance, but describe a given gas or fluid mixture very well, because their
parameters have been adjusted to experimental data.
10. A few closing comments
As one could see, some dearly sold features of dive computers, such as
mountain lake adaption or nitrox ability, are easily implemented within
the model ZH-L16.
To take account of mountain lake adaption, the dive computer has to
measure the ambient pressure in short intervalls and has to recalculate
the tissue saturation accordingly. Ascending to a mountain lake means
nothing more than a reduction in ambient pressure (like surfacing at the
end of a dive, but here the differences in pressure are much less - because
of this there is no need to pay attention to no-decompression or no-stop
times for mountaineers). To support nitrox ability, only the constant for
the nitrogen fraction has to be interchanged by a variable for it, that's
all ! What is necessary, is to adjust the mechanics of the dive computer
(namely the pressure gauge at the first stage) to be (pure-)oxygen compliant.
In particular the difference in price between "no-decompression" and
"deco" dive computers are artificially build up, for it is necessary for a
"no-decompression" computer (for example Uwatec's Aladin Sport) to perform
the decompression calculation (otherwise it could not warn in case of too
fast ascent to the next deco depth !), but it doesn't display all
informations.
We are interested in all questions concerning dive computer. Therefore our
request : please, inform us, if you know more details (literature, URLs, etc.)
about the models used in dive computers. Moreover, other topics are of
great interests : Does anyone know the internal format used by different
dive computers (Suunto, Mares, etc.) ?
Every time we're open to hints, critique and corrections of the surely present
errors. Approval is accepted, too. ;-) In case, this text is used further
anywhere, we would appreciate a short communication from you.
11. Literature, links
- Albert A. Bühlmann und Ernst B. Völlm,
Tauchmedizin: Barotrauma, Gasembolie, Dekompression, Dekompressionskrankheit,
4. Auflage, Springer Verlag 1995
- Peter Bennett and David Elliot,
The Physiology and Medicine of Diving, 4. Ed., W.B. Saunders Company Ltd. 1998
- Schreiner, H.R., and Kelley, P.L.,
A Pragmatic View of Decompression, Underwater Physiology: Proceedings of the
Fourth Symposium on Underwater Physiology, edited by C.J. Lambertsen, Academic Press,
New York 1971, pp. 205-219
-
Haralds Tekkis-Seiten - interesting and well readable informations concerning
diving physics (in German)
-
Bubble Decompression Strategies - Part I : Background and Theory
- recommended article by Eric Maiken concerning bubble models
- Karl Kramers Tec-Page
- comprehensive informations about rebreather und nitrox diving
- Jim Cobb's Trimix Pages
- worth knowing about Trimix
-
Haralds Sauerstoff-Seite - informations concerning diving with pure oxygen
(in German)
- Varying-Permeability Model
- summary of the articles by D.E. Yount and D.C. Hoffman by Kai Schröder (in German)
-
Implications of the Varying Permeability Model for Reverse Dive Profiles
- Artikel von D.E. Yount, E.B. Maiken und E.C. Baker, Manuskript eines Vortrags gehalten beim
Reverse Diving Profiles Workshop on October 29th, and 30th, 1999 in Washington, D.C.
- UDCF - Universal Dive Computer Format
- documentation about the Universal Dive Computer Format by Steffen Reith and Kai Schröder
Links to manufacturers of dive computers :
Formulae translated from TEX by TTH, version 1.0.
